The Hot Hand

The concept of a “hot hand” is a popular one in various sports, and has been variously bunked, debunked and rebunked in numerous contexts. A common manifestation of this idea comes from basketball, where fans routinely feel that players will get “hot” during a stretch of a game during which they make a much higher percentage of their shots than their career average would suggest is likely.

Whether this actually happens is debatable. It’s harder to nail this down than you might think, and numerous people have thrown a fair amount of sophisticated statistics and computing resources at it in baseball and basketball. My understanding of the current state of things is that the “hot hand” effect is generally thought to be dubious, but that there are legitimate questions about whether some of the naysayer’s assumptions are valid^<1.

My approach to this question in biathlon will be fairly rudimentary. So there should be no illusions about me putting this question to bed, at all. Mostly it’ll be a fun opportunity to look at some interesting shooting statistics and maybe learn a little about conditional probability. (Do not be afraid. It will be ok.).

Sadly, I don’t have data on individual shots taken in biathlon races. The best I can do is the number of misses at each shooting stage during each race. If you don’t follow biathlon, skiers alternately ski and shoot. Depending on the length of race, they will shoot 2 or 4 times, split evenly between prone (lying down) and standing (um, not lying down). Each time they shoot, they shoot at five targets. Additionally, the order of prone vs. standing varies between race types.

We end up with four types of races, with the following shooting patterns:

Sprint: Prone Standing
Individual: Prone Standing Prone Standing
Pursuit: Prone Prone Standing Standing
Mass Start: Prone Prone Standing Standing

Again, each time they shoot, they have five targets.

Since I can’t look at each individual target, instead I’ll examine performance from shooting stage to stage, within a particular race. Hitting all five of your targets at a particular stage is called “shooting clean”. My basic question is this: if someone shoots clean, are they more likely to shoot clean at their next shooting stage, in that race.

For starters, let’s just just look at men and women as groups. I took the last five seasons of major international biathlon competitions as my data set. From here, it’s pretty easy to calculate the proportion of times that men and women shoot clean (hit all their targets) shooting prone and standing. I’ll hold off on showing you those numbers to introduce the big wrinkle: it turns out (unsurprisingly) that shooting prone is much easier than shooting standing. Biathletes shoot clean standing at roughly half the rate that they do prone.

The reason this is a problem is that we now need to consider all possible sequences of two shooting stages separately. For example, if you shoot clean at a prone stage, you’re much more likely to shoot clean at the next stage if it’s prone than standing.

So the four cases Prone-Standing, Prone-Prone, Standing-Prone and Standing-Standing need to be considered separately.

Now, finally, I’ll show you the probabilities and then explain them a bit…

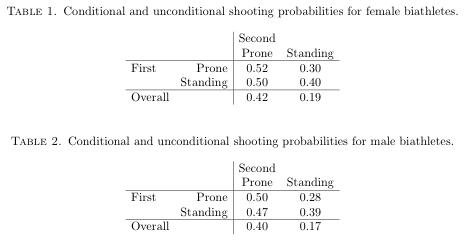Let’s start with the bottom row of each table, the “Overall” row. That’s just the proportion of times men and women shot clean (prone and standing).

The four proportions above these represent the conditional probabilities that we’re interested in. For example, the upper left proportion in the first table, 0.52, is the probability that a female biathlete shoots clean at a prone stage, given that they just shot clean at another prone stage in that same race. Likewise, 0.30 is the probability that a female biathlete shoots clean at a standing stage given that they just shot clean at a prone stage in that same race.

As you can see, men and women both shoot clean prone around 40% of the time, but only shoot clean standing around 17-19% of the time. Proportions should only be compared within each column of each table. So, women shoot clean prone 42% of the time. If they shot clean at the last stage, they’ll shoot clean at a prone stage 52% or 50% of the time, depending on whether the last stage was prone or standing.

The obvious result here is that shooting clean once appears to make it much more likely they’ll shoot clean at the next stage.

However, this is not evidence of a hot hand effect. Recall that I’ve aggregated data over all athletes (within the men/women categories). What we’re actually seeing here is the effect of conditioning on skiers who shoot clean. The group of skiers who’ve shot clean (at all!) will in general be much better shots. This means that these conditional probabilities are really just reflecting the fact that people who shoot clean once tend to be better shots, so they are more likely to shoot clean again.

What we really need to do is look at these same probabilities but calculated for each athlete…

To be continued…